فـاکـتوریـل، تعریف و کاربردها
فـاکـتوریـل، تعریف و کاربردها
در ریاضیات فاکتوریل یک عدد صحیح نامنفی n که به صورت !n نمایش داده می شود، حاصل ضرب تمام اعداد صحیح مثبت کمتر از یا برابر با n است. برای نمونه،

و

نماد !n را کریستین کرامپ (Christian Kramp) در سال 1808 وارد کرد.
تعریف
تابع فاکتوریل به طور قراردادی با فرمول

تعریف می شود. تعریف بالا مورد
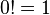
را در خود جای می دهد؛ به عنوان مثالی از این حقیقت که حاصل ضرب هیچ عددی در همه، یک است. این واقعیت برای فاکتوریل مفید است چرا که:
- رابطه بازگشتی  برای n = 0 کار می کند.
برای n = 0 کار می کند.
- بنا کردن عبارتها برای چند جمله ای های نامتناهی را ساده می سازد؛ برای مثال  .
.
- این تعریف، هویت بسیاری از ترکیبها را برای اندازه های صفر معتبر می کند.
- به ویژه، عدد ترکیبات یا جایگشتهای (combinations or permutations) یک مجموعه تهی به سادگی برابر با یک است.
کاربردها
- فاکتوریلها در ترکیبات (combinatorics) به کار می روند. برای مثال، !n راه مختلف برای برای مرتب کردن n شیئی مجزا در یک ترتیب وجود دارد (این آرایه ها جایگشت- permutations- نامیده میشوند). تعداد راههائی که شخص می تواند k شیئی را از میان مجموعه مشخصی از n شیئی انتخاب کند (تعداد ترکیبات)، با ضریب دو جمله ای زیر داده می شود:

- در جایگشت، اگر r شیئی بتوانند از کل n شیئی انتخاب شوند و به طرق مختلفی چیده شوند، وقتی که r کوچکتر یا برابر با n است، آن گاه تعداد کل جایگشتهای مشخص با فرمول زیر داده می شود:

- فاکتوریلها در حساب نیز ظاهر می شوند. برای مثال، قضیه تایلور (Taylor's theorem) تابع (f(x را به شکل سریهای توانی بر حسب x بیان می کند. بر این مبنا که مشتق n ام x به توان n برابر است با !n .
- فاکتوریلها نیز به صورت گسترده در نظریه احتمال به کار برده می شوند.
- فاکتوریلها اغلب هنگام آموزش بازگشت در علم رایانه به عنوان مثال ساده ای همراه با اعداد فیبوناتچی (Fibonacci numbers) استفاده می شوند؛ چرا که رابطه بازگشتی زیر را برآورده می کنند (اگر n بزرگتر یا مساوی یک باشد):

فاکتوريل دوگانه و سري ها
فاکتوريل دوگانه در سري هاي زيباي زير به کار مي رود:
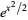 =
= 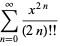
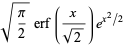 =
= 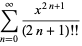
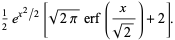 =
= 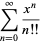
سري زير، مجموع معکوس فاکتوريل هاي دوگانه را به دست مي دهد (از Sloane):
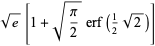 =
= 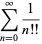
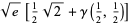 =
=
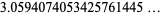 =
=
وقتي که 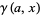 يک تابع گاماي ناقص پائيني است. اين مجموع، مورد خاصي از ثابت چند فاکتوريلي معکوس است.
يک تابع گاماي ناقص پائيني است. اين مجموع، مورد خاصي از ثابت چند فاکتوريلي معکوس است.
رامانويان (Ramanuian) مجموع فشرده اي را به صورت زير ارائه داده است (Hardy 1999, p. 106):
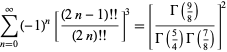
ويپل (Whipple) در سال 1926 تعميم اين مجموع را به دست آورد (Hardy 1999, pp. 111-112).
روابط بين فاکتوريل دوگانه و فاکتوريل عادي
فاکتوريل دوگانه نيز ميتواند به عددهاي صحيح فرد منفي با استفاده از تعريف
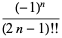 =
= 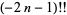
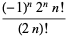 =
=
براي n=0, 1, … (Arfken 1985, p. 547) بسط داده شود.
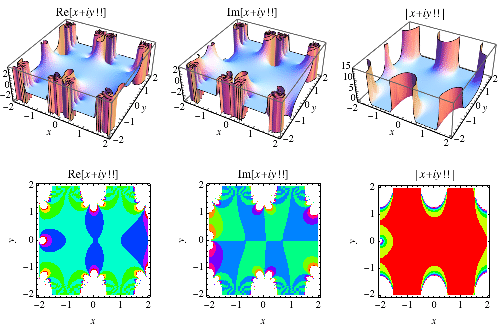
به طور مشابه، فاکتوريل دوگانه ميتواند به آرگومانهاي مختلط به صورت زير بسط يابد:
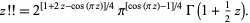
مشخصه هاي بسيار زيادي وجود دارند که فاکتوريل دوگانه را به فاکتوريلها مربوط ميسازند؛ مانند
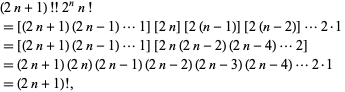
اين رابطه ها به 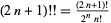 ميرسند. براي n=0, 1, … ، اولين مقدارها عبارتند از
ميرسند. براي n=0, 1, … ، اولين مقدارها عبارتند از
1، 3، 15، 105، 945، 10395 (Sloane). همچنين از آن جا که
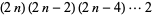 =
= 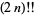
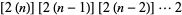 =
=
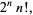 =
=
اين نتيجه ميدهد 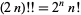 . براي n=0, 1, … ، اولين مقدارها عبارتند از
. براي n=0, 1, … ، اولين مقدارها عبارتند از
1، 2، 8، 48، 384، 3840، 46080 و... (Sloane). در نهايت چون
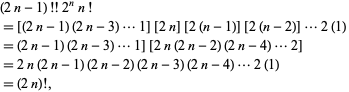
اين رابطه به 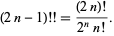 منجر ميشود.
منجر ميشود.
براي n فرد
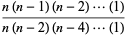 =
= 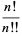
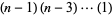 =
=
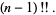 =
=
براي n زوج
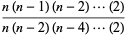 =
= 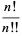
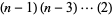 =
=
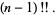 =
=
بنابراين براي هر n
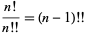
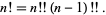
تعريف فاکتوريل دوگانه
فاکتوريل دوگانة يک عدد صحيح مثبت n تعميمي از فاکتوريل عادي n! است و به صورت

تعريف مي شود.
توجه کنيد که بنا بر تعريف ارفکن داريم !!0 = !! 1- (Arfken 1985, p. 547). نمادگذاري n!! به صورت گسترده شناخته نشده است و در Cajori ذکري از آن به ميان نيامده است (Cajori, 1993).
براي n = 0, 1, 2, … نخستين مقدارها عبارتند از 1، 1، 2، 3، 8، 15، 48، 105، 384 و ... (Sloane). تعداد رقمهاي دهدهي در !!(10n) براي n=0, 1, … عبارتند از
1، 4، 80، 1285، 17831، 228289، 2782857، 32828532 و... (Sloane).
فاکتوريل دوگانه در Mathematica به شکل n!! يا Factorial2 آمده است.
فاکتوريل دوگانه مورد ويژه اي از چندفاکتوريل (مالتي فاکتوريل multifactorial) به شمار ميرود.
فاکتوريل دوگانه مي تواند بر حسب تابع گاما و به شکل
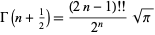
بيان شود (Arfken 1985, p. 548).
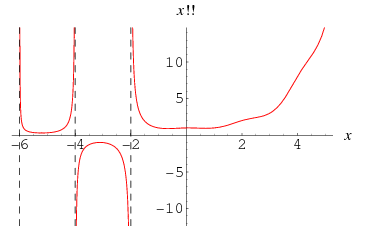
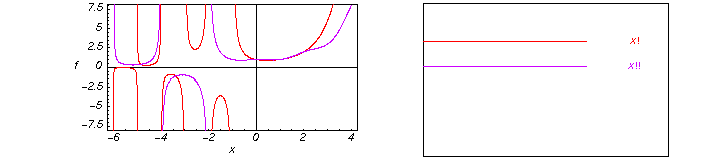
نمودارهاي ! x و !! x در يک محور مختصاتي